Volume of Cone Formula Derivation Solved Examples

Volume Cone is a three-dimensional geometric shape .its circular base tapers smoothly to a point called the apex or vertex of the cone. It can be seen as a set of asymmetric circular discs stacked on top of each other, the ratio of the radii of adjacent discs being constant. The line segment joining is a vertex of the cone to the center of the circular base. Then, it is called the height of the cone. The circular bases’ radius is called the cone’s radius (r). 

The length of the line segment joining at the vertex to any point of the circumference of a circular base is called the cone’s slant height (l). The right circular cone is a cone with its vertex above the circular base. When it is not specified as a ‘cone,’ it is usually referred to as a right circular cone.

Volume of Cone

The volume of a cone defines the area or capacity of the cone. A cone is a three-dimensional geometric shape with a circular base from a flat base to a point called the apex or apex. A cone is formed by line segments, bisectors, or lines connecting a common point, a vertex, and all non-vertex points. Cone can be seen in the set of asymmetric circular discs so that the ratio of the radii of adjacent discs is constant.

Examples of Cones are Pencil tips, Funnel, Ice cream cones, Birthday caps, and others.

The volume of cones in real life

We come across various cone-shaped objects in our daily life. What is the volume of the cone? Or how to find it? The volume of a cone helps find the sizes of cone-shaped objects. Some of them are:

• Traffic cones
• Ice-cream cones
• Funnels
• Christmas Tree
• Birthday caps

Volume of Cone Formula

The volume of the cone formula is given by the circular base and one-third of the cone. According to geometrical and mathematical concepts, a cone can be described as a pyramid with a circular cross-section. Measuring the height and radius of the cone, you can easily find the volume of the cone. The radius of the base of the cones is “r,” and the height of a cone is “h”, then the volume of a cone is given as V = (1/3)πr2h.

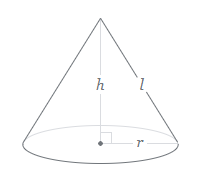
• ‘r’ is the base radius of the cone.
• ‘l’ is a slant height of the cone.
• ‘h’ is the height of the cone.

As we can see from the cone formula above, a cone’s capacity is one-third of a cylinder’s capacity. If we take 1/3rd of the volume of the cylinder, we get the formula for the volume of the cone.

Volume of Cone Derivation

Cone is a triangle rotated around one of its vertices. Now, e can think of a scenario where we have to calculate the amount of water held in a conical flask. In other words, To calculate the capacity of this flask. The capacity of a conical flask is equal to the volume of the cone involved. Therefore, a three-dimensional shape’s volume equals the space occupied by that shape. Let’s do an activity to calculate the volume of a cone.

Take one cylindrical container and a conical flask of the same height and base radius. Add water to a conical flask filled to the brim. Start adding this water to the cylindrical container you have taken. You will notice that it does not fill the container. Try repeating this experiment one more time. You will still notice some space in the container.

Let us know its formula now. Suppose a cone has a circular base of radius ‘r’ and its height is ‘h’. The volume of this cone is equal to one-third of the product of the area of ​​the base and its height.

V = 1/3 x circular base x height of cone

Since we know about the area of ​​a circle by the formula, the base of a cone has an area (say B)B = πr2Hence, substituting this value, we get;

V = 1/3 x πr2 x h.

V is volume, r is radius and h is height.

How to Find Volume of Cone?

The volume of a cone is calculated by applying the volume of a cone formula. The steps below can be followed when the cone’s base radius or base diameter, height, and slant height are known.

Step 1: Note the known parameters of cone base, radius ‘r’, diameter ‘d’, slant height ‘L’ and height ‘h.’

Step 2: Use the formula to find the volume of the cone,

The volume of a cone using base radius: V = (1/3)πr2h or (1/3)πr2√(L2 – r2)

Volume of cone using base diameter: V = (1/12)πd2h = (1/12)πd2√(L2 – r2).

Step 3: show the obtained result in cubic units.

Volume of Cone Tips

.The volume of a hemisphere of radius “r” is equal to that of a cone of radius “r” and height ‘2r’. Thus, (1/3)πr2(2r) = (2/3)πr3.

.The volume of a cone is calculated by using the diameter by dividing the diameter by two and then applying the value in the volume of the cone formula (1/3)πr2h to find the radius.

CONCLUSION

The volume of a cone is derived from its sibling “cylinder”. Consider a cylinder of height “h” and radius “r”. The volume of the cylinder is pi∗r2∗h. Make a cone of the same height “h” and radius “r”. The volume of regular cones and pyramids is 1/3 of the formula.

The formula for the volume of a simple cylinder is that the area of ​​the base of the cylinder is greater than the height of the cylinder and that a cylinder decomposes into three cones, each of equal volume; Thus, the volume of each cone is 1/3 the volume of the cylinder.